Color

Red
Black
Red는 동시에 2개가 나올 수 없다.

NODE_TYPE

PARENT : 부모 노드
LCHILD : 왼쪽 자식 노드
RCHILD : 오른쪽 자식 노드

RBPair

트리에 들어갈 자료형
int key, int value 타입

Node

트리에 들어갈 노드

#pragma once
#include<assert.h>
/*
1. 모든 노드는 빨간색 혹은 검은색이다.
2. 루트 노드는 검은색이다.
3. 모든 리프 노드(NIL)들은 검은색이다. (NIL : null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드)
4. 빨간색 노드의 자식은 검은색이다.   == No Double Red(빨간색 노드가 연속으로 나올 수 없다)
5. 모든 리프 노드에서 Black Depth는 같다.   == 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.

G(Grand Parent) = 조부모 노드
P(Parent) = 부모 노드
U(Uncle) = 삼촌 노드 (부모의 형제 노드)
N(New) = 삽입 노드

삽입 과정
- 삽입 시 항상 빨간색으로 삽입 됨.
=> 4번 조건이 위배되는 상황 발생
=> 삼촌 노드가 검은색이라면 -> Restructuring
=> 삼촌 노드가 빨간색이라면 -> Recoloring 수행

Restructuring
1. N, P, G를 오름차순 정렬
2. 셋 중 중간 값을 부모로 만들고 나머지 둘을 자식으로 만듬
3. 새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 만든다.

Recoloring
1. 새로운 노드(N)의 부모(P)와 삼촌(U)를 검은색으로 바꾸고 조상(G)를 빨간색으로 바꾼다
1-1. 조상(G)이 루트 노드라면 검은색으로 바꾼다.
1-2. 조상(G)를 빨간색으로 바꿨을 떄 또다시 Double Red가 발생한다면 
또다시 Restructring 혹은 Recoloring을 진행해서 Double Red 문제가 발생하지 않을 때까지 반복한다.
*/

enum class Color
{
	RED,
	BLACK,
	END
};

enum class NODE_TYPE
{
	PARENT,			// 1
	LCHILD,			// 2
	RCHILD,			// 3
	END				// 4
};

struct RBPair
{
	// data
	int first;
	int second;
};

RBPair make_rbpair(const int& _first, const int& _second)
{
	return RBPair{ _first, _second };
}

class RBTree
{
public:
	class Node
	{

	private:
		RBTree*		rbTree;
		Node*		arrNode[(int)NODE_TYPE::END];
		RBPair		data;
		Color		color;

	public:
		explicit Node(RBTree* rbTree, RBPair data)
			: rbTree(rbTree)
			, data(data)
			, color(Color::RED)
			, arrNode{nullptr, nullptr, nullptr}
		{
			
		}

		explicit Node(RBTree* rbTree)
			: rbTree(rbTree)
			, data()
			, color(Color::BLACK)
			, arrNode{nullptr, nullptr, nullptr}
		{

		}
	public:
		bool isNil() const
		{
			if (this == this->rbTree->m_Nil)
			{
				return true;
			}

			return false;
		}

		bool isRoot() const
		{
			if (isNil())
			{
				return false;
			}

			if (nullptr == this->arrNode[(int)NODE_TYPE::PARENT])
			{
				return true;
			}

			return false;
		}

		bool isLeftChild() const
		{
			if (isRoot() || isNil())
			{
				return false;
			}

			if (this == this->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD])
			{
				return true;
			}

			return false;
		}

		bool isRightChild() const
		{
			if (isRoot() || isNil())
			{
				return false;
			}

			if (this == this->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD])
			{
				return true;
			}
		}

		friend class RBTree;
	};

... 생략
	

};

arrNode : 노드에 연결된 부모, 왼, 오른쪽 자식 저장
data : RBPair 데이터
color : 노드의 색상
나머지 멤버 함수들은 헬퍼 함수.

RBTree

선언부

#pragma once
#include<assert.h>
/*
1. 모든 노드는 빨간색 혹은 검은색이다.
2. 루트 노드는 검은색이다.
3. 모든 리프 노드(NIL)들은 검은색이다. (NIL : null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드)
4. 빨간색 노드의 자식은 검은색이다.   == No Double Red(빨간색 노드가 연속으로 나올 수 없다)
5. 모든 리프 노드에서 Black Depth는 같다.   == 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.

G(Grand Parent) = 조부모 노드
P(Parent) = 부모 노드
U(Uncle) = 삼촌 노드 (부모의 형제 노드)
N(New) = 삽입 노드

삽입 과정
- 삽입 시 항상 빨간색으로 삽입 됨.
=> 4번 조건이 위배되는 상황 발생
=> 삼촌 노드가 검은색이라면 -> Restructuring
=> 삼촌 노드가 빨간색이라면 -> Recoloring 수행

Restructuring
1. N, P, G를 오름차순 정렬
2. 셋 중 중간 값을 부모로 만들고 나머지 둘을 자식으로 만듬
3. 새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 만든다.

Recoloring
1. 새로운 노드(N)의 부모(P)와 삼촌(U)를 검은색으로 바꾸고 조상(G)를 빨간색으로 바꾼다
1-1. 조상(G)이 루트 노드라면 검은색으로 바꾼다.
1-2. 조상(G)를 빨간색으로 바꿨을 떄 또다시 Double Red가 발생한다면
또다시 Restructring 혹은 Recoloring을 진행해서 Double Red 문제가 발생하지 않을 때까지 반복한다.
*/

enum class Color
{
	RED,
	BLACK,
	END
};

enum class NODE_TYPE
{
	PARENT,			// 1
	LCHILD,			// 2
	RCHILD,			// 3
	END				// 4
};

struct RBPair
{
	// data
	int key;
	int value;
};

RBPair make_rbpair(const int& _key, const int& _value)
{
	return RBPair{ _key, _value };
}

class RBTree
{
public:
	class Node
	{

	private:
		RBTree* rbTree;
		Node* arrNode[(int)NODE_TYPE::END];
		RBPair		data;
		Color		color;

	public:
		explicit Node(RBTree* rbTree, RBPair data)
			: rbTree(rbTree)
			, data(data)
			, color(Color::RED)
			, arrNode{ nullptr, nullptr, nullptr }
		{

		}

		explicit Node(RBTree* rbTree)
			: rbTree(rbTree)
			, data()
			, color(Color::BLACK)
			, arrNode{ nullptr, nullptr, nullptr }
		{

		}
	public:
		bool isNil() const
		{
			if (this == this->rbTree->m_Nil)
			{
				return true;
			}

			return false;
		}

		bool isRoot() const
		{
			if (isNil())
			{
				return false;
			}

			if (nullptr == this->arrNode[(int)NODE_TYPE::PARENT])
			{
				return true;
			}

			return false;
		}

		bool isLeftChild() const
		{
			if (isRoot() || isNil())
			{
				return false;
			}

			if (this == this->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD])
			{
				return true;
			}

			return false;
		}

		bool isRightChild() const
		{
			if (isRoot() || isNil())
			{
				return false;
			}

			if (this == this->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD])
			{
				return true;
			}
		}

		friend class RBTree;
	};

public:
	RBTree()
		: m_Root(nullptr)
		, m_Nil(new Node{ this })
		, m_Count(0)
	{

	}

	~RBTree()
	{

	}

	// 멤버 변수 (private)
private:
	Node* m_Root;		// root node
	Node* m_Nil;		// nil node
	int				m_Count;	// 데이터 개수

	// 멤버 함수 (private)
private:
	void rotateLeft(Node* node);
	void rotateRight(Node* node);
	void fixInsert(Node* node);
	void transplant(Node* u, Node* v);
	RBTree::Node* minimum(Node* node);
	void fixDelete(Node* node);

public:
	void insert(RBPair data);
	void deleteKey(int key);
	void search(int key);

};

NIL 노드

경계 노드 ⇒ RedBlackTree에서 NULL에 해당하는 부분을 나타내는 노드이며 색상은 Black을 나타낸다. Red-Black Tree의 규칙 중 모든 leaf 노드는 검은색이다 라는 규칙을 항상 지킬 수 있기 위한 방법이다.

보조 함수

helper 함수

isLeftChild(node)
{
	if (node->parent->left == node)
	{
			return true;
	}
	return false;
}

isRightChild(node)
{
	if (node->parent->right == node)
	{
		return true;
	}

	return false;
}

isRoot(node)
{
	if (node->parent == nil)
	{
		return true;
	}

	return false;
}

우회전(RotateRight)

우회전 구현

rotateRight(tree, parent)
{
	left_child = parent->left;
	parent->left = left_child->right;
	
	grand_parent = parent->parent;
	left_child->parent = grand_parent;

	if (true == parent->isLeftChild())
		grand_parent->left = left_child;
	else if (true == parent->isRightChild())
		grand_parent->right = left_child;
	else
		tree->root = left_child;

	
	left_child->right = parent;
	parent->parent = left_child;
}

좌회전(RotateLeft)

좌회전 구현

void RBTree::rotateLeft(Node* parent)
{
	Node* right_child = parent->arrNode[(int)NODE_TYPE::RCHILD];

	// 1. 서브트리 대입, 부모 변경
	parent->arrNode[(int)NODE_TYPE::RCHILD] = right_child->arrNode[(int)NODE_TYPE::LCHILD];
	right_child->arrNode[(int)NODE_TYPE::LCHILD]->arrNode[(int)NODE_TYPE::PARENT] = parent;
	right_child->arrNode[(int)NODE_TYPE::PARENT] = parent->arrNode[(int)NODE_TYPE::PARENT];

	// 2. 조부모의 자식 변경
	if (parent->isLeftChild())
	{
		parent->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = right_child;
	}
	else if (parent->isRightChild())
	{
		parent->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = right_child;
	}
	else if (parent->isRoot())
	{
		right_child->rbTree->m_Root = right_child;
	}

	// 3. 자식노드와 부모노드의 위치 변경.
	parent->arrNode[(int)NODE_TYPE::PARENT] = right_child;
	right_child->arrNode[(int)NODE_TYPE::LCHILD] = parent;

}

Restructring

Restuctring은 Double Red에서 Uncle 노드가 검정색일 떄 발생한다.
Restructuring은 다음 과정을 거친다.

새로운 노드(N), 부모 노드(P), 조상 노드(G)를 오름차순으로 정렬한다.
셋 중 중간 값을 부모로 만들고 나머지 둘을 자식으로 만든다.
새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 만든다.

1단계

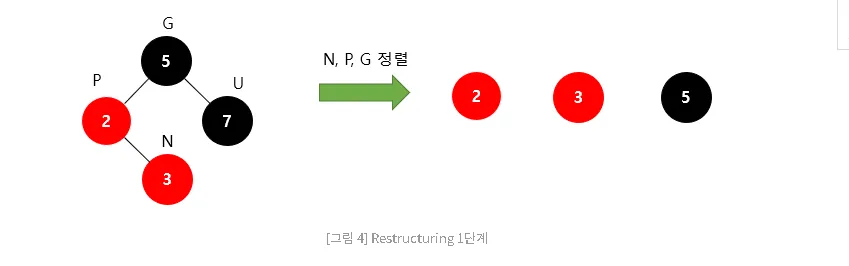
2단계

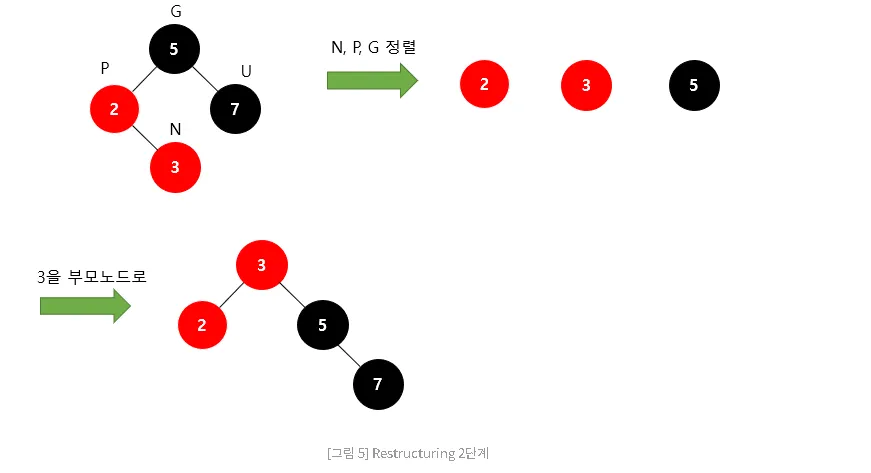
3단계

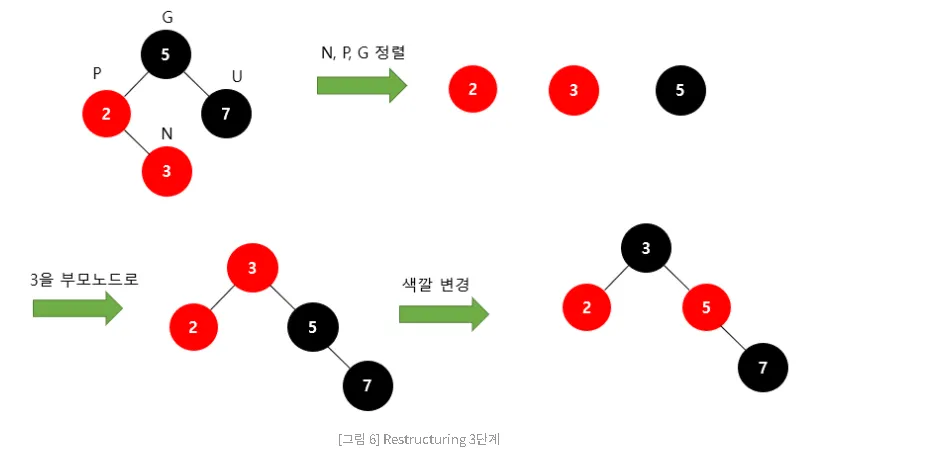
Recoloring

ReColoring은 다음 과정을 거친다.

새로운 노드(N)의 부모(P)와 삼촌(U)을 검은색으로 바꾸고 조상(G)을 빨간색으로 바꾼다.
1-1. 조상(G)이 루트 노드라면 검은색으로 바꾼다.
1-2. 조상(G)을 빨간색으로 바꿨을 때 또다시 Double Red가 발생한다면 또다시 Restructuring 혹은 Recoloring을 진행해서 Double Red 문제가 발생하지 않을 때까지 반복한다.

Red-BlackTree의 삭제.

공통

이진 탐색 트리의 삭제와 동일한 과정을 거친다.
연결 관계를 수정하고 대체 노드를 반환한다. (원래 삭제 노드의 자리에 대체 노드 넣기)

Case : 삭제 노드의 색상이 Red 일 떄

추가 작업이 없다.

Case : 삭제 노드의 색상이 black 일 때

대체 노드의 색상을 black으로 변경한다.

Case A: 대체 노드의 색상이 Red일 때

대체 노드의 색상을 black으로 변경하고 종료한다.

Case B: 대체 노드의 색상이 black일 때

대체 노드가 왼쪽 자식인 경우만 확인 대체 노드가 이중 흑색노드가 된다.

이중 흑색 노드의 형제가 RED인 경우
- 형제를 검은색, 부모를 빨간색으로 칠한다. 부모 노드를 기준으로 좌회전 한다.
- 대체 노드는 여전히 이중 흑색 노드이다.
이중 흑색 노드의 형제가 BLACK 이고 형제의 양쪽 자식 모두 BLACK인 경우
- 형제노드만 RED로 만들고, 이중 흑색노드의 검은색 1개를 부모에게 전달.
- 부모가 RED인 경우 색칠 후 끝
- 부모가 BLACK인 경우 이중 흑색 노드가 생성되었으므로 다시 CASE별 반복
이중 흑색노드의 형제가 BLACK이고 형제의 왼쪽 자식이 RED, 오른쪽 자식이 BLACK인 경우
- 형제노드를 RED로, 형제노드의 왼쪽 자식을 BLACK으로 칠한 후에 형제노드를 기준으로 우회전한다.
이중 흑색노드의 형제가 BLACK이고 형제의 오른쪽 자식이 RED인 경우
- 부모 노드의 색을 형제에게 넘긴다.
- 부모 노드와 형제노드의 오른쪽 자식을 검은색으로 칠한다.
- 부모 노드 기준으로 좌회전한다.

Red-BlackTreee 선언부

#pragma once
#include<assert.h>
#include<map>
#include<iostream>
/*
1. 모든 노드는 빨간색 혹은 검은색이다.
2. 루트 노드는 검은색이다.
3. 모든 리프 노드(NIL)들은 검은색이다. (NIL : null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드)
4. 빨간색 노드의 자식은 검은색이다.   == No Double Red(빨간색 노드가 연속으로 나올 수 없다)
5. 모든 리프 노드에서 Black Depth는 같다.   == 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.

G(Grand Parent) = 조부모 노드
P(Parent) = 부모 노드
U(Uncle) = 삼촌 노드 (부모의 형제 노드)
N(New) = 삽입 노드

삽입 과정
- 삽입 시 항상 빨간색으로 삽입 됨.
=> 4번 조건이 위배되는 상황 발생
=> 삼촌 노드가 검은색이라면 -> Restructuring
=> 삼촌 노드가 빨간색이라면 -> Recoloring 수행

Restructuring
1. N, P, G를 오름차순 정렬
2. 셋 중 중간 값을 부모로 만들고 나머지 둘을 자식으로 만듬
3. 새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 만든다.

Recoloring
1. 새로운 노드(N)의 부모(P)와 삼촌(U)를 검은색으로 바꾸고 조상(G)를 빨간색으로 바꾼다.
1-1. 조상(G)이 루트 노드라면 검은색으로 바꾼다.
1-2. 조상(G)를 빨간색으로 바꿨을 떄 또다시 Double Red가 발생한다면
또다시 Restructring 혹은 Recoloring을 진행해서 Double Red 문제가 발생하지 않을 때까지 반복한다.
*/

enum class Color
{
	BLACK,
	RED,
	END
};

enum class NODE_TYPE
{
	PARENT,			// 1
	LCHILD,			// 2
	RCHILD,			// 3
	END				// 4
};

struct RBPair
{

public:
	// data
	int key;
	int value;

	RBPair()
		: key()
		, value()
	{

	}

	RBPair(const int& _key, const int& _value)
		: key(_key)
		, value(_value)
	{

	}

};

class RBTree
{
public:
	class Node
	{

	public:
		RBTree*		rbTree;
		Node*		arrNode[(int)NODE_TYPE::END];
		RBPair		data;
		Color		color;

	public:
		// 일반 노드
		explicit Node(RBTree* rbTree, RBPair data)
			: rbTree(rbTree)
			, data(data)
			, color(Color::RED)
			, arrNode{ rbTree->m_Nil, rbTree->m_Nil, rbTree->m_Nil }
		{

		}

		// NIL 노드
		explicit Node(RBTree* rbTree)
			: rbTree(rbTree)
			, data()
			, color(Color::BLACK)
			, arrNode{ nullptr, nullptr, nullptr }
		{

		}
	public:
		bool isNil() const;
		bool isRoot() const;
		bool isLeftChild() const;
		bool isRightChild() const;

		friend class RBTree;
	};

public:
	RBTree()
		: m_Nil(new Node{ this })
		, m_Root(m_Nil)
		, m_Count(0)
	{

	}

	~RBTree()
	{
		deleteTree(this->m_Root);

		delete m_Nil;
	}

	// 멤버 변수 (private)
public:
	RBTree::Node*	m_Nil;		// nil node
	RBTree::Node*	m_Root;		// root node
	int				m_Count;	// 데이터 개수

	// 멤버 함수 (private)
private:
	void			rotateLeft(RBTree::Node* parent);
	void			rotateRight(RBTree::Node* parent);
	void			fixInsert(RBTree::Node* node);
	void			fixDelete(RBTree::Node* transplant);
	RBTree::Node*	deleteHelp(RBTree::Node* node);
	RBTree::Node*	searchMinNode(RBTree::Node* node);
	void			deleteTree(Node* node);

public:
	bool			insert(RBPair data);
	bool			deleteKey (int key);
	RBTree::Node*	searchNode(int key);

};

Red-BlackTree 구현부

#include "rb_tree.h"

RBPair make_rbpair(const int& _key, const int& _value)
{
	return RBPair{ _key, _value };
}

void RBTree::rotateLeft(RBTree::Node* parent)
{
	Node* right_child = parent->arrNode[(int)NODE_TYPE::RCHILD];

	// 1. 서브트리 대입, 부모 변경
	parent->arrNode[(int)NODE_TYPE::RCHILD] = right_child->arrNode[(int)NODE_TYPE::LCHILD];
	right_child->arrNode[(int)NODE_TYPE::LCHILD]->arrNode[(int)NODE_TYPE::PARENT] = parent;
	right_child->arrNode[(int)NODE_TYPE::PARENT] = parent->arrNode[(int)NODE_TYPE::PARENT];

	// 2. 조부모의 자식 변경
	if (parent->isLeftChild())
	{
		parent->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = right_child;
	}
	else if (parent->isRightChild())
	{
		parent->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = right_child;
	}
	else if (parent->isRoot())
	{
		right_child->rbTree->m_Root = right_child;
	}

	// 3. 자식노드와 부모노드의 위치 변경.
	parent->arrNode[(int)NODE_TYPE::PARENT] = right_child;
	right_child->arrNode[(int)NODE_TYPE::LCHILD] = parent;

}

void RBTree::rotateRight(RBTree::Node* parent)
{
	Node* left_child = parent->arrNode[(int)NODE_TYPE::LCHILD];
	 
	// 1. 서브트리 대입, 부모 변경
	parent->arrNode[(int)NODE_TYPE::LCHILD] = left_child->arrNode[(int)NODE_TYPE::RCHILD];
	left_child->arrNode[(int)NODE_TYPE::RCHILD]->arrNode[(int)NODE_TYPE::PARENT] = parent;
	left_child->arrNode[(int)NODE_TYPE::PARENT] = parent->arrNode[(int)NODE_TYPE::PARENT];

	// 2. 조부모의 자식 변경
	if (parent->isLeftChild())
	{
		parent->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = left_child;
	}
	else if (parent->isRightChild())
	{
		parent->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = left_child;
	}
	else if(parent->isRoot())
	{
		left_child->rbTree->m_Root = left_child;
	}
	
	// 3. 자식노드와 부모노드의 위치 변경.
	parent->arrNode[(int)NODE_TYPE::PARENT] = left_child;
	left_child->arrNode[(int)NODE_TYPE::RCHILD] = parent;
}

void RBTree::fixInsert(RBTree::Node* node)
{

	Node* parent = nullptr;
	Node* uncle = nullptr;
	// 부모의 Color가 Red라면
	while (Color::RED == node->arrNode[(int)NODE_TYPE::PARENT]->color)
	{
		parent = node->arrNode[(int)NODE_TYPE::PARENT];

		if (parent->isLeftChild())
		{
			uncle = parent->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD];

			// ReColoring
			if (Color::RED == uncle->color)
			{
				parent->color = Color::BLACK;
				uncle->color = Color::BLACK;
				parent->arrNode[(int)NODE_TYPE::PARENT]->color = Color::RED;
				node = parent->arrNode[(int)NODE_TYPE::PARENT];
			}
			else
			{
				if (node->isRightChild())
				{
					node = node->arrNode[(int)NODE_TYPE::PARENT];
					rotateLeft(node);
				}

				node->arrNode[(int)NODE_TYPE::PARENT]->color = Color::BLACK;
				node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::PARENT]->color = Color::RED;
				rotateRight(node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::PARENT]);
			}
		}
		else
		{
			uncle = parent->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD];

			if (uncle->color == Color::RED)
			{
				parent->color = Color::BLACK;
				uncle->color = Color::BLACK;
				parent->arrNode[(int)NODE_TYPE::PARENT]->color = Color::RED;
				node = parent->arrNode[(int)NODE_TYPE::PARENT];
			}
			else
			{
				if (node->isLeftChild())
				{
					// node -> parent로 이동.
					node = node->arrNode[(int)NODE_TYPE::PARENT];
					rotateRight(node);
				}

				node->arrNode[(int)NODE_TYPE::PARENT]->color = Color::BLACK;
				node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::PARENT]->color = Color::RED;
				rotateLeft(node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::PARENT]);
			}

		}
	}

	node->rbTree->m_Root->color = Color::BLACK;

}

void RBTree::fixDelete(RBTree::Node* transplant)
{	

	// 2. 대체 노드의 색상이 검은색인 경우 
	Node* sibling = this->m_Nil;
	while (!transplant->isRoot() && transplant->color == Color::BLACK)
	{
		if (transplant->isLeftChild())
		{
			sibling = transplant->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD];

			if (sibling->color == Color::RED)
			{
				// 1. 형제가 빨간색인 경우
				
				sibling->color = Color::BLACK;
				transplant->arrNode[(int)NODE_TYPE::PARENT]->color = Color::RED;
				rotateLeft(transplant->arrNode[(int)NODE_TYPE::PARENT]);
			}
			else
			{
				// 2. 형제가 검은색인 경우

				if (sibling->arrNode[(int)NODE_TYPE::LCHILD]->color == Color::BLACK && sibling->arrNode[(int)NODE_TYPE::RCHILD]->color == Color::BLACK)
				{
					// A. 형제의 양쪽 자식이 모두 검은색인 경우
					sibling->color = Color::RED;
					transplant = transplant->arrNode[(int)NODE_TYPE::PARENT];
				}
				else if (sibling->arrNode[(int)NODE_TYPE::LCHILD]->color == Color::RED && sibling->arrNode[(int)NODE_TYPE::RCHILD]->color == Color::BLACK)
				{
					// B. 형제의 왼쪽 자식은 빨간색, 오른쪽 자식은 검은색인 경우.
					sibling->color = Color::RED;
					sibling->arrNode[(int)NODE_TYPE::LCHILD]->color = Color::BLACK;
					rotateRight(sibling);
					sibling = transplant->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD];
				}
				else
				{
					// C. 형제가 검은색이고 형제의 오른쪽 자식이 빨간색인 경우
					sibling->color = sibling->arrNode[(int)NODE_TYPE::PARENT]->color;
					transplant->arrNode[(int)NODE_TYPE::PARENT]->color = Color::BLACK;
					sibling->arrNode[(int)NODE_TYPE::RCHILD]->color = Color::BLACK;
					rotateLeft(transplant->arrNode[(int)NODE_TYPE::PARENT]);
					transplant = this->m_Root;
				}
			}

		}
		else if (transplant->isRightChild())
		{
			sibling = transplant->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD];

			if (sibling->color == Color::RED)
			{
				// 1. 형제가 빨간색인 경우

				sibling->color = Color::BLACK;
				transplant->arrNode[(int)NODE_TYPE::PARENT]->color = Color::RED;
				rotateRight(transplant->arrNode[(int)NODE_TYPE::PARENT]);
			}
			else
			{
				// 2. 형제가 검은색인 경우

				if (sibling->arrNode[(int)NODE_TYPE::LCHILD]->color == Color::BLACK && sibling->arrNode[(int)NODE_TYPE::RCHILD]->color == Color::BLACK)
				{
					// A. 형제의 양쪽 자식이 모두 검은색인 경우
					sibling->color = Color::RED;
					transplant->arrNode[(int)NODE_TYPE::PARENT]->color = Color::BLACK;
				}
				else if (sibling->arrNode[(int)NODE_TYPE::LCHILD]->color == Color::BLACK && sibling->arrNode[(int)NODE_TYPE::RCHILD]->color == Color::RED)
				{
					// B. 형제의 오른쪽 자식은 빨간색, 왼쪽 자식은 검은색인 경우.
					sibling->color = Color::RED;
					sibling->arrNode[(int)NODE_TYPE::RCHILD]->color = Color::BLACK;
					rotateLeft(sibling);
					sibling = transplant->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD];
				}
				else
				{
					// C. 형제가 검은색이고 형제의 왼쪽 자식이 빨간색인 경우
					sibling->color = sibling->arrNode[(int)NODE_TYPE::PARENT]->color;
					transplant->arrNode[(int)NODE_TYPE::PARENT]->color = Color::BLACK;
					sibling->arrNode[(int)NODE_TYPE::LCHILD]->color = Color::BLACK;
					rotateRight(transplant->arrNode[(int)NODE_TYPE::PARENT]);
					transplant = this->m_Root;
				}
			}
		}
	}
}

RBTree::Node* RBTree::deleteHelp(RBTree::Node* node)
{
	// 대체 노드 반환.

	// 사용할 임시 노드.
	RBTree::Node* curNode = node->rbTree->m_Nil;

	if (node->arrNode[(int)NODE_TYPE::LCHILD]->isNil() && node->arrNode[(int)NODE_TYPE::RCHILD]->isNil())
	{
		//  1. 리프노드일 경우.
		if (node->isRoot())
		{
			node->rbTree->m_Root = node->rbTree->m_Nil;
		}
		else if (node->isLeftChild())
		{
			node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = node->rbTree->m_Nil;
		}
		else if (node->isRightChild())
		{
			node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = node->rbTree->m_Nil;
		}
	}
	else if (!node->arrNode[(int)NODE_TYPE::LCHILD]->isNil() && node->arrNode[(int)NODE_TYPE::RCHILD]->isNil())
	{
		// 2. 왼쪽 서브트리만 가지고 있을 경우. => 왼쪽 서브트리에서 가장 큰 값을 가져온다.
		curNode = node->arrNode[(int)NODE_TYPE::LCHILD];

		while (true)
		{
			if (curNode->arrNode[(int)NODE_TYPE::RCHILD]->isNil())
			{
				break;
			}
			curNode = curNode->arrNode[(int)NODE_TYPE::RCHILD];
		}

		if (curNode->isLeftChild())
		{
			// 삭제 노드의 왼쪽 서브트리에 오른쪽 자식이 없는 경우.
			curNode->arrNode[(int)NODE_TYPE::PARENT] = node->arrNode[(int)NODE_TYPE::PARENT];
		}
		else if (curNode->isRightChild())
		{
			// 대체 노드에게 왼쪽 자식이 있는 경우
			if (!curNode->arrNode[(int)NODE_TYPE::LCHILD]->isNil())
			{
				curNode->arrNode[(int)NODE_TYPE::LCHILD]->arrNode[(int)NODE_TYPE::PARENT] = curNode->arrNode[(int)NODE_TYPE::PARENT];
				curNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = curNode->arrNode[(int)NODE_TYPE::LCHILD];
			}
			else
			{
				// 대체 노드에게 자식이 없는 경우.

				// 대체 노드 연결관계 수정
				curNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = node->rbTree->m_Nil;
			}

			// 삭제 노드 연결관계 수정 => 삭제노드는 왼쪽 서브트리만을 가지고 있음.
			node->arrNode[(int)NODE_TYPE::LCHILD]->arrNode[(int)NODE_TYPE::PARENT] = curNode;
			curNode->arrNode[(int)NODE_TYPE::LCHILD] = node->arrNode[(int)NODE_TYPE::LCHILD];
			curNode->arrNode[(int)NODE_TYPE::PARENT] = node->arrNode[(int)NODE_TYPE::PARENT];
		}

		// 삭제 노드의 위치
		if (node->isRoot())
		{
			node->rbTree->m_Root = curNode;
		}
		else if (node->isRightChild())
		{
			node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = curNode;
		}
		else if (node->isLeftChild())
		{
			node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = curNode;
		}
	}
	else if (!node->arrNode[(int)NODE_TYPE::RCHILD]->isNil() && node->arrNode[(int)NODE_TYPE::LCHILD]->isNil())
	{
		// 3. 오른쪽 서브트리만 가지고 있을 경우. => 오른쪽 서브트리에서 가장 작은 값을 가져온다.
		curNode = node->arrNode[(int)NODE_TYPE::RCHILD];

		// 오른쪽 서브트리의 가장 왼쪽으로 이동.
		while (true)
		{
			if (nullptr == curNode->arrNode[(int)NODE_TYPE::LCHILD])
			{
				break;
			}
			curNode = curNode->arrNode[(int)NODE_TYPE::LCHILD];
		}

		if (curNode->isRightChild())
		{
			// 삭제 대상노드의 오른쪽 서브트리에 왼쪽 자식이 없는 경우
			curNode->arrNode[(int)NODE_TYPE::PARENT] = node->arrNode[(int)NODE_TYPE::PARENT];
		}
		else if (curNode->isLeftChild())
		{
			// 삭제 대상노드의 오른쪽 서브트리에 왼쪽 자식이 있는 경우

			// 대체 노드에게 오른쪽 자식이 있는 경우
			if (!curNode->arrNode[(int)NODE_TYPE::RCHILD]->isNil())
			{
				// 대체 노드 자식 연결관계 수정
				curNode->arrNode[(int)NODE_TYPE::RCHILD]->arrNode[(int)NODE_TYPE::PARENT] = curNode->arrNode[(int)NODE_TYPE::PARENT];
				curNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = curNode->arrNode[(int)NODE_TYPE::RCHILD];
			}
			else
			{
				// 대체 노드 연결관계 수정
				curNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = nullptr;
			}

			// 삭제 노드 연결관계 수정 => 삭제 노드는 오른쪽 서브트리만을 가지고 있음.
			node->arrNode[(int)NODE_TYPE::RCHILD]->arrNode[(int)NODE_TYPE::PARENT] = curNode;
			curNode->arrNode[(int)NODE_TYPE::RCHILD] = node->arrNode[(int)NODE_TYPE::RCHILD];

			curNode->arrNode[(int)NODE_TYPE::PARENT] = node->arrNode[(int)NODE_TYPE::PARENT];
		}

		if (node->isRoot())
		{
			node->rbTree->m_Root = curNode;
		}
		else if (node->isRightChild())
		{
			node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = curNode;
		}
		else if (node->isLeftChild())
		{
			node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = curNode;
		}
	}
	else if (!node->arrNode[(int)NODE_TYPE::RCHILD]->isNil() && !node->arrNode[(int)NODE_TYPE::LCHILD]->isNil())
	{
		// 4. 양쪽 노드가 모두 존재할 경우.
		curNode = node->arrNode[(int)NODE_TYPE::RCHILD];

		while (true)
		{
			if (nullptr == curNode->arrNode[(int)NODE_TYPE::LCHILD])
			{
				break;
			}

			curNode = curNode->arrNode[(int)NODE_TYPE::LCHILD];

		}

		if (curNode->isRightChild())
		{
			// 삭제 대상노드의 오른쪽 서브트리에 왼쪽 자식이 없는 경우 (오른쪽 연결은 되어있음).
			curNode->arrNode[(int)NODE_TYPE::PARENT] = node->arrNode[(int)NODE_TYPE::PARENT];
			curNode->arrNode[(int)NODE_TYPE::LCHILD] = node->arrNode[(int)NODE_TYPE::LCHILD];
			node->arrNode[(int)NODE_TYPE::LCHILD]->arrNode[(int)NODE_TYPE::PARENT] = curNode;
		}
		else if (curNode->isLeftChild())
		{
			// 삭제 대상노드의 오른쪽 서브트리에 왼쪽 자식이 있는 경우

			// 대체 노드에게 오른쪽 자식이 있는 경우
			if (!curNode->arrNode[(int)NODE_TYPE::RCHILD]->isNil())
			{
				// 대체 노드 자식 연결관계 수정
				curNode->arrNode[(int)NODE_TYPE::RCHILD]->arrNode[(int)NODE_TYPE::PARENT] = curNode->arrNode[(int)NODE_TYPE::PARENT];
				curNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = curNode->arrNode[(int)NODE_TYPE::RCHILD];
			}
			// 대체 노드에게 오른쪽 자식이 없는 경우.
			else
			{
				// 대체 노드 연결관계 수정
				curNode->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = node->rbTree->m_Nil;
			}

			// 삭제 노드 연결관계 수정 => 삭제 노드는 오른쪽, 왼쪽 서브 트리를 모두 가지고 있음.
			node->arrNode[(int)NODE_TYPE::RCHILD]->arrNode[(int)NODE_TYPE::PARENT] = curNode;
			curNode->arrNode[(int)NODE_TYPE::RCHILD] = node->arrNode[(int)NODE_TYPE::RCHILD];

			node->arrNode[(int)NODE_TYPE::LCHILD]->arrNode[(int)NODE_TYPE::PARENT] = curNode;
			curNode->arrNode[(int)NODE_TYPE::LCHILD] = node->arrNode[(int)NODE_TYPE::LCHILD];

			curNode->arrNode[(int)NODE_TYPE::PARENT] = node->arrNode[(int)NODE_TYPE::PARENT];
		}

		if (node->isRoot())
		{
			node->rbTree->m_Root = curNode;
		}
		else if (node->isRightChild())
		{
			node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD] = curNode;
		}
		else if (node->isLeftChild())
		{
			node->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD] = curNode;
		}

	}

	return curNode;
}

RBTree::Node* RBTree::searchMinNode(RBTree::Node* node)
{
	if (node->isNil())
	{
		return this->m_Nil;
	}
	
	if (node->arrNode[(int)NODE_TYPE::LCHILD]->isNil())
	{
		return node;
	}

	return searchMinNode(node->arrNode[(int)NODE_TYPE::LCHILD]);

}

void RBTree::deleteTree(Node* node)
{	
	if (!node->arrNode[(int)NODE_TYPE::LCHILD]->isNil())
	{
		deleteTree(node->arrNode[(int)NODE_TYPE::LCHILD]);
	}
	else if (!node->arrNode[(int)NODE_TYPE::RCHILD]->isNil())
	{
		deleteTree(node->arrNode[(int)NODE_TYPE::RCHILD]);
	}
	
	node->arrNode[(int)NODE_TYPE::LCHILD] = this->m_Nil;
	node->arrNode[(int)NODE_TYPE::RCHILD] = this->m_Nil;

	if (!node->isNil())
	{
		delete node;
	}
	
}

bool RBTree::insert(RBPair data)
{
	Node* newNode = new Node{ this, data };
	// 1. root가 없는 경우
	if (this->m_Root->isNil())
	{
		this->m_Root = newNode;
		return true;
	}

	Node* curNode = this->m_Root;
	// 2. 삽입

	while (true)
	{
		if (curNode->data.key == newNode->data.key)
		{
			return false;
		}
		else if (curNode->data.key < newNode->data.key)
		{
			if (this->m_Nil == curNode->arrNode[(int)NODE_TYPE::RCHILD])
			{
				// 삽입 시점.
				curNode->arrNode[(int)NODE_TYPE::RCHILD] = newNode;
				newNode->arrNode[(int)NODE_TYPE::PARENT] = curNode;
				break;
			}
			else
			{
				// 이동 시점.
				curNode = curNode->arrNode[(int)NODE_TYPE::RCHILD];
			}
		}
		else if (curNode->data.key > newNode->data.key)
		{
			if (this->m_Nil == curNode->arrNode[(int)NODE_TYPE::LCHILD])
			{
				// 삽입 시점.
				curNode->arrNode[(int)NODE_TYPE::LCHILD] = newNode;
				newNode->arrNode[(int)NODE_TYPE::PARENT] = curNode;
				break;
			}
			else
			{
				// 이동 시점.
				curNode = curNode->arrNode[(int)NODE_TYPE::LCHILD];
			}
		}
	}
	fixInsert(newNode);
	++this->m_Count;

	return true;

}

bool RBTree::deleteKey(int key)
{
	RBTree::Node* transplant = this->m_Nil;

	// 1. 삭제할 노드 선정.
	RBTree::Node* target = searchNode(key);
	

	if (target->isNil())
	{
		return false;
	}

	// 2. 이식 노드 찾기. => 이진 탐색트리로서의 연결관계 수정이 일어난다.
	transplant= deleteHelp(target);

	if (target->color == Color::BLACK)
	{
		// 3. 노드의 색상이 검은색이면 balance 작업 => 이중 흑색노드 정상화.
		fixDelete(transplant);
	}
	else
	{
		// 4. 빨간색인 경우 검정색으로 칠해줌.
		transplant->color = Color::BLACK;
	}
	
	delete target;

	--transplant->rbTree->m_Count;

	return true;
}

RBTree::Node* RBTree::searchNode(int key)
{
	// 이진 탐색 트리 삭제.

	// 1. 비었는지 체크.
	if (this->m_Root->isNil())
	{
		std::cout << "Tree가 비어있음." << std::endl;
		return this->m_Nil;
	}

	// 2. 탐색
	Node* node = this->m_Root;

	while (true)
	{
		if (node->isNil())
		{
			std::cout << "찾고자 하는 Key가 존재하지 않음." << std::endl;
			return node;
		}
		else if (node->data.key > key)
		{
			// 왼쪽 이동.
			node = node->arrNode[(int)NODE_TYPE::LCHILD];
		}
		else if (node->data.key < key)
		{
			// 오른쪽 이동.
			node = node->arrNode[(int)NODE_TYPE::RCHILD];
		}
		else if (node->data.key == key)
		{
			break;
		}
	}

	return node;
}

bool RBTree::Node::isNil() const
{
	if (this == this->rbTree->m_Nil)
	{
		return true;
	}

	return false;
}

bool RBTree::Node::isRoot() const
{
	if (isNil())
	{
		return false;
	}

	if (this->rbTree->m_Nil == this->arrNode[(int)NODE_TYPE::PARENT])
	{
		return true;
	}

	return false;
}

bool RBTree::Node::isLeftChild() const
{
	if (isRoot() || isNil())
	{
		return false;
	}

	if (this == this->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::LCHILD])
	{
		return true;
	}

	return false;
}

bool RBTree::Node::isRightChild() const
{
	if (isRoot() || isNil())
	{
		return false;
	}

	if (this == this->arrNode[(int)NODE_TYPE::PARENT]->arrNode[(int)NODE_TYPE::RCHILD])
	{
		return true;
	}

	return false;
}

'C++' 카테고리의 다른 글

C++ 동적 할당 (0)	2024.12.14
C++ 자료구조 구현 이중 원형 연결 리스트 (0)	2024.12.07
C++ 클래스 (0)	2024.05.12
C++ 동적할당 (0)	2024.05.04
C++ 컴파일 과정 (0)	2024.04.21

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

그냥

C++ 자료구조 구현 Red-Black Tree

Color

NODE_TYPE

RBPair

Node

RBTree

선언부

NIL 노드

보조 함수

우회전(RotateRight)

좌회전(RotateLeft)

Restructring

Recoloring

Red-BlackTree의 삭제.

공통

Case : 삭제 노드의 색상이 Red 일 떄

Case : 삭제 노드의 색상이 black 일 때

Case A: 대체 노드의 색상이 Red일 때

Case B: 대체 노드의 색상이 black일 때

Red-BlackTreee 선언부

Red-BlackTree 구현부

'C++' 카테고리의 다른 글

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역

C++ 자료구조 구현 Red-Black Tree

Color

NODE_TYPE

RBPair

Node

RBTree

선언부

NIL 노드

보조 함수

우회전(RotateRight)

좌회전(RotateLeft)

Restructring

Recoloring

Red-BlackTree의 삭제.

공통

Case : 삭제 노드의 색상이 Red 일 떄

Case : 삭제 노드의 색상이 black 일 때

Case A: 대체 노드의 색상이 Red일 때

Case B: 대체 노드의 색상이 black일 때

Red-BlackTreee 선언부

Red-BlackTree 구현부

'C++' 카테고리의 다른 글

'C++' Related Articles

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역